jar形式のファイルは、JDKがインストールされている環境であれば、 以下の方法で展開することができます。
C:>jar xvf src.jar |
その後、
C:>javac *.java |
としてコンパイルします。もし、JDK1.4以降のJDKを使用していて、 MicrosoftのVMで実行したい場合は、
C:>javac -target 1.1 *.java |
としてください。
その後、reversi.htmlをブラウザまたはappletviewerで開けば、 リバーシ・ゲームを開始できます。
正直、ここで提供しているリバーシゲームの思考ルーチンはさほど強くない (作者がこの手のゲームはド下手なのもありまして…(^^;)のですが、 一応アルゴリズムを説明しておきます。
このリバーシゲームのコンピュータの思考ルーチンでは、 ミニマックス法とαβ枝刈りを使用しています。
この手のゲームの思考ルーチンでは、盤面を何手か先まで先読みします。 先読みした上で、どの手を選ぶかを選択する戦略のひとつがミニマックス法です。
ミニマックス法では、再帰呼び出しを使用して取り得る手を探索し、 ある程度の深さまで先読みした所で、その盤面の「評価値」を求めます。 評価値とは、その盤面がどの程度自分にとって有利であるかを表す値です。 そして、再帰呼び出しの帰り道で、敵の打つ局面では、 評価値が最も低いものを選択し、自分が打つ局面では、 最も高いものを選択します。 敵が自分に有利になるようなことをするはずがないからです。
ミニマックス法は、リバーシゲームのような思考ゲームでは 定番と言えるアルゴリズムです。 また、αβ法は、探索の枝を刈りこんで、 結果を変えずに所要時間を短縮するための手法です。
ミニマックス法やαβ枝刈りは定番のアルゴリズムですので、 思考ルーチンを強くする肝になるのは、 盤面の評価値を求める関数(評価関数)であると言えるでしょう。
このリバーシゲームでは、以下のようにして評価値を求めています。
基本値の計算
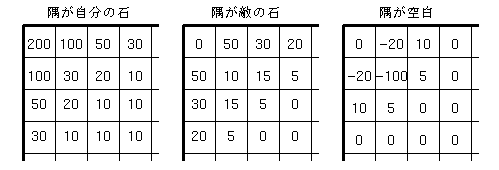
基本値は、各セルの評価値表を参照し、自分の石がある場合、 敵の石がある場合の評価値を合計することで算出します。
ただし、各セルの評価値は隅に石があるかないかで変動します。 隅を取られないためには、隅に隣接するセルには置かない方がよいですが、 隅が埋まった後には気にする必要がないためです。 そこで、隅の状態により、評価値表を盤面の1/4毎に差し替えています。

正直、この評価値表は、根拠なし超テキトー検証もなしのシロモノですが…
着手数・要石の計算
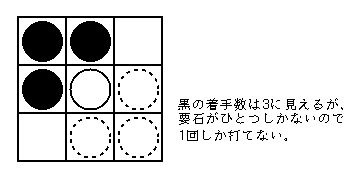
リバーシゲームでは打てる所がある限りパスが許されませんから、 手詰りで不利な個所に打たないように、 着手数(石が置ける場所の数)は多ければ多いほど有利です。
しかし、一見着手数が多いように見えても、 ひっくり返す敵の石がひとつしかなければ、結局一度しか使えない。 そこで、着手数と同時に、 その手によりひっくり返される石(要石)の数も考慮に入れています。
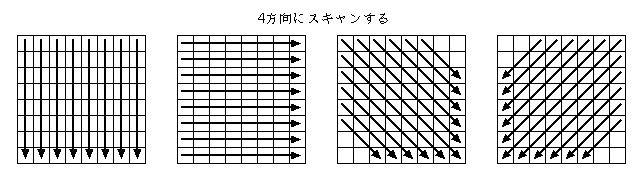
着手数・要石を計算するのに、 全てのセルから8方向にスキャンしていたのでは時間がかかるので、 本プログラムでは盤面に対して4方向にスキャンし、 盤面と同サイズの2次元配列にフラグを立てるようにしています。
端の確定石
4方向スキャンのどの方向でも返されない石のうち、 特に盤の端のものを確定石と考え、カウントしています。 ---が、現在は、カウントしているだけで評価には使っていません。
参考文献